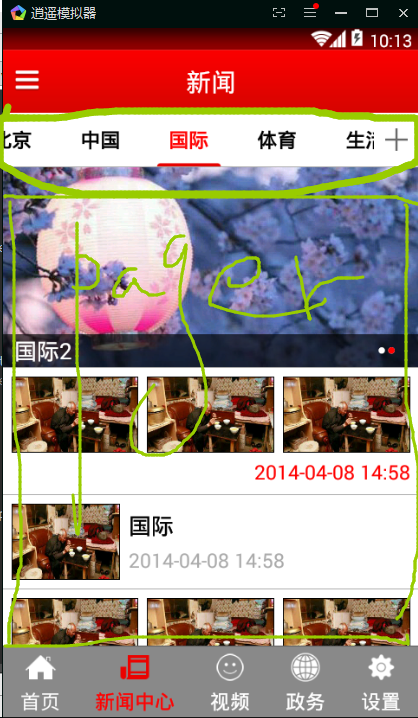
TabPagerIndicator使用
本文共 1433 字,大约阅读时间需要 4 分钟。
 1 注意/在清单文件中配置activity/theme=
1 注意/在清单文件中配置activity/theme=
android:theme="@style/Theme.PageIndicatorDefaults">
// 2 (adpter中添加getPageTitle)
2 (adpter中添加getPageTitle)
//1.给viewPager设置数据适配器 MyPagerAdapter myPagerAdapter = new MyPagerAdapter(); pager.setAdapter(myPagerAdapter); //2.指示器和viewPager进行绑定 indicator.setViewPager(pager);
3 重点(修改选中文字的颜色,背景) values/style/tabPageIndicator
values/style/tabPageIndicator
@android:color/transparent 为加背景,,不能用@null
<item name="vpiTabPageIndicatorStyle">@style/Widget.TabPageIndicator</item>//这里
</style>
<style name="Widget"> </style> <style name="Widget.TabPageIndicator" parent="Widget"> <item name="android:gravity">center</item><item name="android:background">@drawable/vpi__tab_indicator</item>//背景
<item name="android:paddingLeft">22dip</item> <item name="android:paddingRight">22dip</item> <item name="android:paddingTop">12dp</item> <item name="android:paddingBottom">12dp</item> <item name="android:textAppearance">@style/TextAppearance.TabPageIndicator</item> <item name="android:textSize">12sp</item> <item name="android:maxLines">1</item> </style> <style name="TextAppearance.TabPageIndicator" parent="Widget"> <item name="android:textStyle">bold</item><item name="android:textColor">@color/vpi__dark_theme</item>//文字颜色
</style> <style name="Widget.IconPageIndicator" parent="Widget"> <item name="android:layout_marginLeft">6dp</item> <item name="android:layout_marginRight">6dp</item> </style></resources>
你可能感兴趣的文章
nessus快速安装使用指南(非常详细)零基础入门到精通,收藏这一篇就够了
查看>>
Nessus漏洞扫描教程之配置Nessus
查看>>
Nest.js 6.0.0 正式版发布,基于 TypeScript 的 Node.js 框架
查看>>
nestJS学习
查看>>
NetApp凭借领先的混合云数据与服务把握数字化转型机遇
查看>>
NetBeans IDE8.0需要JDK1.7及以上版本
查看>>
netcat的端口转发功能的实现
查看>>
netfilter应用场景
查看>>
netlink2.6.32内核实现源码
查看>>
Netpas:不一样的SD-WAN+ 保障网络通讯品质
查看>>
NetScaler的常用配置
查看>>
netsh advfirewall
查看>>
NETSH WINSOCK RESET这条命令的含义和作用?
查看>>
Netty WebSocket客户端
查看>>
netty 主要组件+黏包半包+rpc框架+源码透析
查看>>
Netty 异步任务调度与异步线程池
查看>>
Netty中集成Protobuf实现Java对象数据传递
查看>>
Netty事件注册机制深入解析
查看>>
Netty原理分析及实战(四)-客户端与服务端双向通信
查看>>
Netty和Tomcat的区别已经性能对比
查看>>